3.1.2.2. A model of the sodium channel: Introducing CellML encapsulation and interfaces¶
The HH sodium channel has two types of gate, an \(m\) gate (of which there are 3) that is initially closed (\(m = 0\)) before activating and inactivating back to the closed state, and an \(h\) gate that is initially open (\(h = 1\)) before activating and inactivating back to the open state. The short period when both types of gate are open allows a brief window current to pass through the channel. Therefore,
where \(\bar{g}_{\text{Na}} = \ \)120 mS.cm-2, and with \(\left\lbrack \text{Na}^{+} \right\rbrack_{i}\)= 30mM and \(\left\lbrack \text{Na}^{+} \right\rbrack_{o}\)= 140mM, the Nernst potential for the sodium channel (z=1) is
The gating kinetics are described by
where the voltage dependence of these four rate constants is determined experimentally to be[1]
Before we construct a CellML model of the sodium channel, we first introduce some further CellML concepts that help deal with the complexity of biological models: first the use of encapsulation groups and public and private interfaces to control the visibility of information in modular CellML components. To understand encapsulation, it is useful to use the terms ‘parent’, ‘child’ and ‘sibling’.
def group as encapsulation for
comp sodium_channel incl
comp sodium_channel_m_gate;
comp sodium_channel_h_gate;
endcomp;
enddef;
We define the CellML components sodium_channel_m_gate and sodium_channel_h_gate below. Each of these components has its own equations (voltage-dependent gates and first order gate kinetics) but they are both parts of one protein – the sodium channel – and it is useful to group them into one sodium_channel component as shown above:
We can then talk about the sodium channel as the parent of two children: the m gate and the h gate, which are therefore siblings. A private interface allows a parent to talk to its children and a public interface allows siblings to talk among themselves and to their parents (see Fig. 3.11).
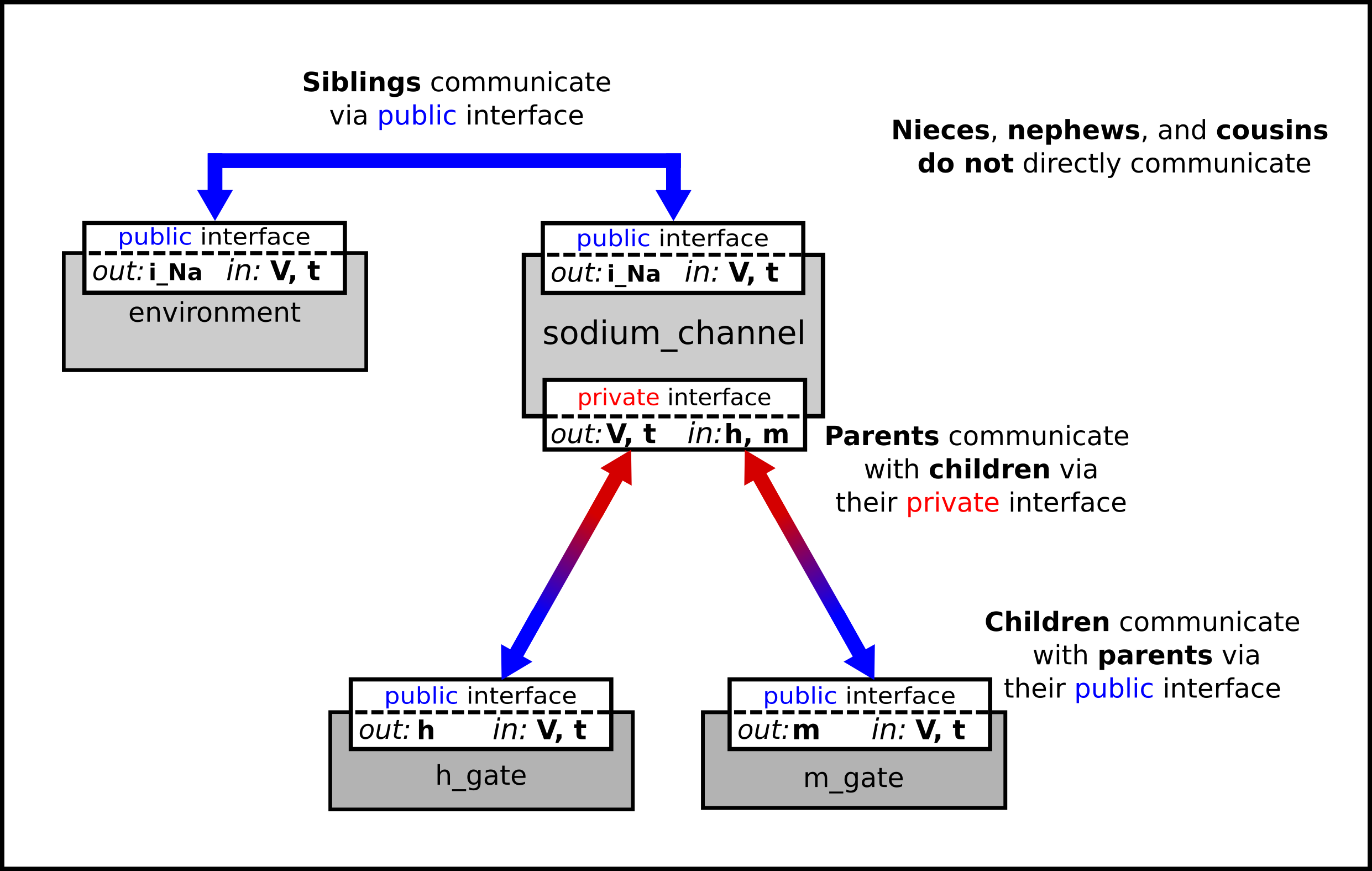
Fig. 3.11 Children talk to each other as siblings, and to their parents, via public interfaces. But the outside world can only talk to children through their parents via a private interface. Note that the siblings m_gate and h_gate could talk via a public interface but only if a mapping is established between them (not needed here).
The OpenCOR CellML Text for the HH sodium ion channel is given below.
def model sodium_ion_channel as
def unit millisec as
unit second {pref: milli};
enddef;
def unit per_millisec as
unit second {pref: milli, expo: -1};
enddef;
def unit millivolt as
unit volt {pref: milli};
enddef;
def unit per_millivolt as
unit millivolt {expo: -1};
enddef;
def unit per_millivolt_millisec as
unit per_millivolt;
unit per_millisec;
enddef;
def unit microA_per_cm2 as
unit ampere {pref: micro};
unit metre {pref: centi, expo: -2};
enddef;
def unit milliS_per_cm2 as
unit siemens {pref: milli};
unit metre {pref: centi, expo: -2};
enddef;
def unit mM as
unit mole {pref: milli};
enddef;
def comp environment as
var V: millivolt {pub: out};
var t: millisec {pub: out};
V = sel
case (t > 5 {millisec}) and (t < 15 {millisec}):
-20.0 {millivolt};
otherwise:
-85.0 {millivolt};
endsel;
enddef;
def group as encapsulation for
comp sodium_channel incl
comp sodium_channel_m_gate;
comp sodium_channel_h_gate;
endcomp;
enddef;
def comp sodium_channel as
var V: millivolt {pub: in, priv: out};
var t: millisec {pub: in, priv: out };
var m: dimensionless {priv: in};
var h: dimensionless {priv: in};
var g_Na: milliS_per_cm2 {init: 120};
var i_Na: microA_per_cm2 {pub: out};
var Nao: mM {init: 140};
var Nai: mM {init: 30};
var RTF: millivolt {init: 25};
var E_Na: millivolt;
var Na_conductance: milliS_per_cm2 {pub: out};
E_Na=RTF*ln(Nao/Nai);
Na_conductance = g_Na*pow(m, 3{dimensionless})*h;
i_Na= Na_conductance*(V-E_Na);
enddef;
def comp sodium_channel_m_gate as
var V: millivolt {pub: in};
var t: millisec {pub: in};
var alpha_m: per_millisec;
var beta_m: per_millisec;
var m: dimensionless {init: 0.05, pub: out};
alpha_m = 0.1{per_millivolt_millisec}*(V+25{millivolt})
/(exp((V+25{millivolt})/10{millivolt})-1{dimensionless});
beta_m = 4{per_millisec}*exp(V/18{millivolt});
ode(m, t) = alpha_m*(1{dimensionless}-m)-beta_m*m;
enddef;
def comp sodium_channel_h_gate as
var V: millivolt {pub: in};
var t: millisec {pub: in};
var alpha_h: per_millisec;
var beta_h: per_millisec;
var h: dimensionless {init: 0.6, pub: out};
alpha_h = 0.07{per_millisec}*exp(V/20{millivolt});
beta_h = 1{per_millisec}/(exp((V+30{millivolt})/10{millivolt})+1{dimensionless});
ode(h, t) = alpha_h*(1{dimensionless}-h)-beta_h*h;
enddef;
def map between environment and sodium_channel for
vars V and V;
vars t and t;
enddef;
def map between sodium_channel and sodium_channel_m_gate for
vars V and V;
vars t and t;
vars m and m;
enddef;
def map between sodium_channel and sodium_channel_h_gate for
vars V and V;
vars t and t;
vars h and h;
enddef;
enddef;
The results of the OpenCOR computation, with Ending point 40 and Point interval 0.1, are shown in Fig. 3.12 with plots \(V\left( t \right)\), \(m\left( t \right)\), \(h\left( t \right)\), \(g_{\text{Na}}\left( t \right)\) and \(i_{\text{Na}}(t)\) for voltage steps from (a) -85mV to -20mV, (b) -85mV to 0mV and (c) -85mV to 20mV. There are several things to note:
- The kinetics of the m-gate are much faster than the h-gate.
- The opening behaviour is faster as the voltage is stepped to higher values since \(\tau = \frac{1}{\alpha_{n} + \beta_{n}}\) reduces with increasing V (see Fig. 3.7).
- The sodium channel conductance rises (activates) and then falls (inactivates) under a positive voltage step from rest since the three m-gates turn on but the h-gate turns off and the conductance is a product of these. Compare this with the potassium channel conductance shown in Fig. 3.10 which is only reduced back to zero by stepping the voltage back to its resting value – i.e. deactivating it.
- The only time current \(i_{\text{Na}}\) flows through the sodium channel is during the brief period when the m-gate is rapidly opening and the much slower h-gate is beginning to close. A small current flows during the reverse voltage step but this is at a time when the h-gate is now firmly off so the magnitude is very small.
- The large sodium current \(i_{\text{Na}}\) is an inward current and hence negative.
Note that the bottom trace does not quite line up at t=0 because the values shown on the axes are computed automatically and hence can take more or less space depending on their magnitude.
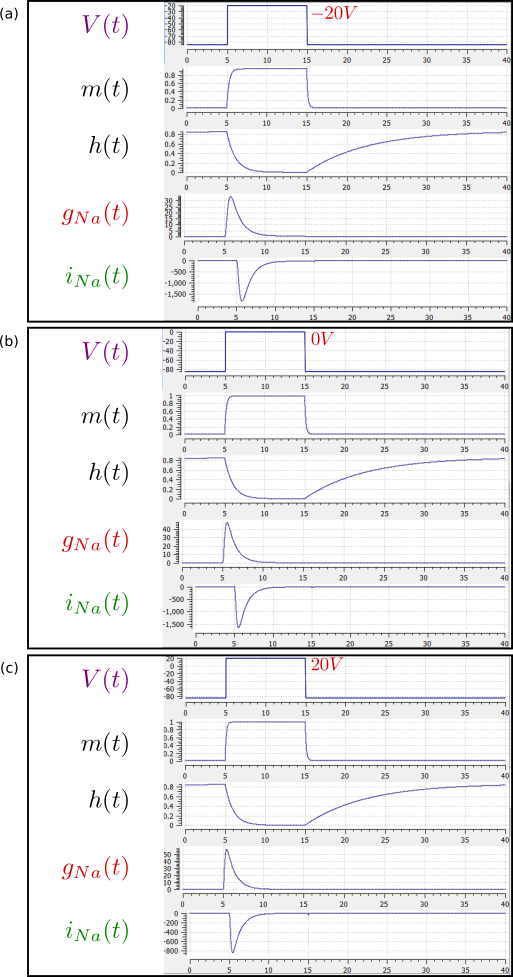
Fig. 3.12 Kinetics of the sodium channel gates for voltage steps to (a) -20mV, (b) 0mV (OpenCOR link), and (c) 20mV.
Footnotes
| [1] | The HH paper used \(\alpha_m\ =\ \frac{0.1(v+25)}{e^{\frac{(v+25)}{10}}-1}\); \(\beta_m\ =\ 4e^{\frac{v}{18}}\); \(\alpha_h\ =\ 0.07e^{\frac{v}{20}}\); \(\beta_h\ =\ \frac{1}{e^{\frac{(v+30)}{10}}+1}\);. |